Masonry Shell Structures with Discrete Equivalence ClassesSIGGRAPH 2023, technical paper (journal track) |

Figure 1: A masonry shell structure modeled by our approach, in which 181 shell elements fall into 60 discrete equivalence classes. Shell elements in the same class have exactly the same shape and are rendered with the same color.
Abstract
Masonry shell structures have been built for centuries around the world in the form of arches, domes and vaults, due to their advantages like large span, lightweight, and high strength. The shapes of masonry shells are generally described by 3D curved surfaces since the thickness of these structures is significantly smaller compared to its width and length. From a geometric perspective, a masonry shell is a geometric tiling of a 3D surface with a number of shell elements that contact one another with no overlaps and no gaps. To tile a freeform 3D surface, it is likely that each shell element has a unique shape when compared to the other elements, requiring each element to be custom manufactured.
In this paper, we study a new problem of modeling freeform shell structures where the shell elements fall into a set of discrete equivalence classes. The major technical challenge in this process is balancing the desire for high reusability of template elements with the need for a seamless and buildable final structure. To address the challenge, we define three error metrics to measure the seamlessness and buildability of shell structures made from discrete equivalence classes and develop a hierarchical cluster-and-optimize approach to generate a small set of template elements that produce a structure closely approximating the surface with low error metrics. We demonstrate the feasibility of our approach on various freeform surfaces and geometric patterns, and validate buildability of our results with four physical results.
Download
Paper PDF (~45.4M)Supplementary PDF (~7.1M)
Supplementary Data (~7.1M)
Source Code
Video
Results

Figure 2: Our approach allows generating results with a variety of patterns on a Dome surface by lifting 2D tessellations (see the boxed images) using a shape-preserving mapping. The 2D tessellations in the top, middle, and bottom rows are monohedral, dihedral, trihedral tilings, respectively. For each result, shell elements falling in the same discrete equivalence class are rendered with the same color.

Figure 3: Our approach allows generating results from a variety of freeform guiding surfaces. From left to right and then top to bottom: Arcuation, Curved Surface, Canopy, Monkey Saddle, Roof, Blob, Arch, Snow, Vouga Surface, Botanic Bubble, Pentagon, and Aquadom.
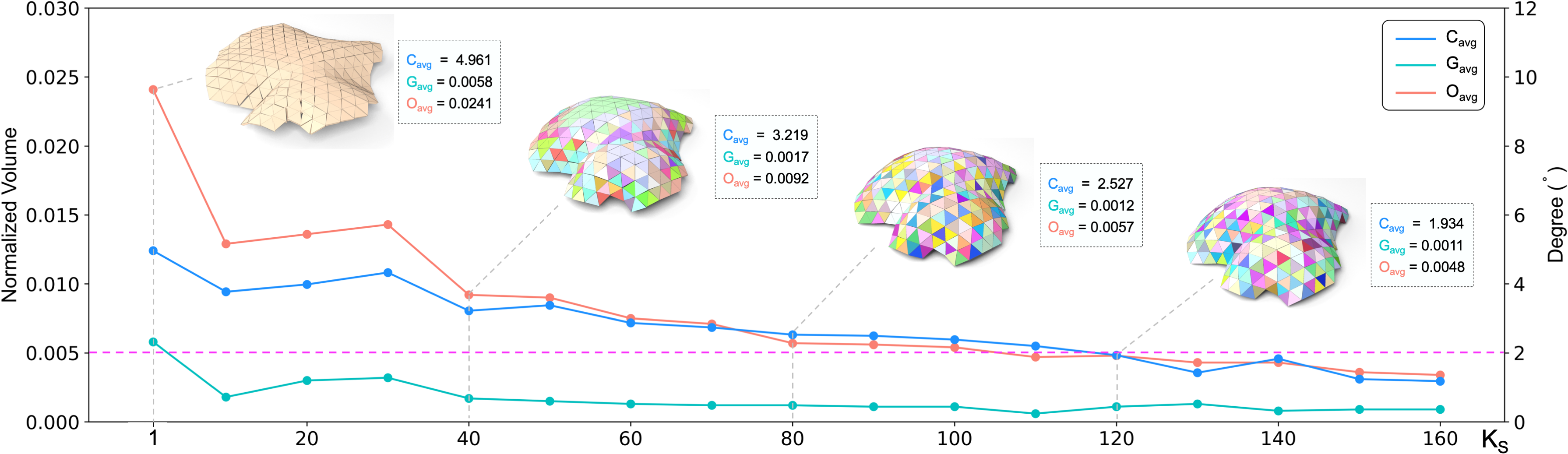
Figure 4: Average errors of the three metrics decrease when a larger number of template elements are allowed to model a shell structure with N = 328 elements. Few template elements lead to obvious gaps and overlaps in the structure; see the left two sampled results. The horizontal purple line indicates the thresholds that we set on the error metrics.

Figure 5: 3D printed shell elements and assembled shell structures. Shell elements in the same class are painted with the same color.
Acknowledgments
We thank the reviewers for their valuable comments, and Zebin Chen for helping on preparing some 3D surface models and renderings. This work was supported by the SUTD grant RS-INSUR-00027, the Ministry of Education, Singapore, under its Academic Research Fund Grants (RG20/20 & MOE-T2EP20220-0014), and the Royal Society (IES\R3\193208).
Bibtex
@article {Chen-2023-TileableShell,author = {Rulin Chen and Pengyun Qiu and Peng Song and Bailin Deng and Ziqi Wang and Ying He},
title = {Masonry Shell Structures with Discrete Equivalence Classes},
journal = {ACM Transactions on Graphics (SIGGRAPH)},
volume = {42},
number = {4},
year = {2023}}