Inverse Tiling of 2D Finite DomainsSIGGRAPH Asia 2025, conference paper |
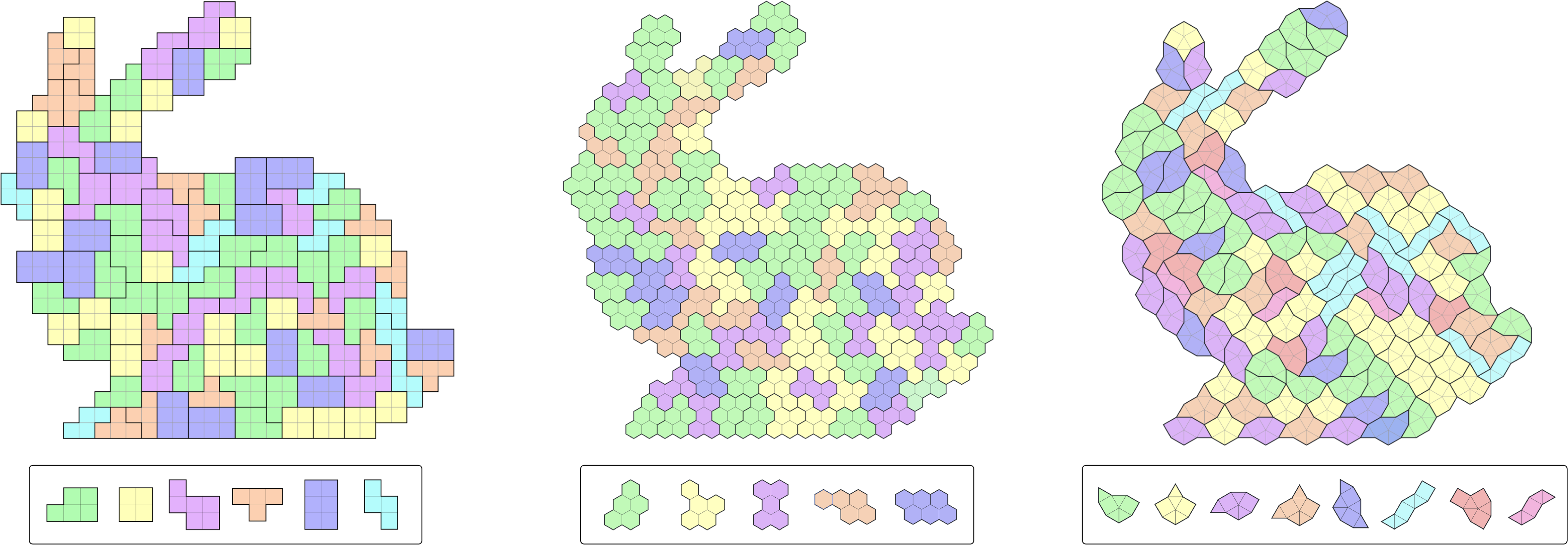
Figure 1: Three K-hedral tiling results produced by our inverse tiling approach. To effectively tile each of the 2D finite domains shown above, our approach constructs a minimized set of distinct tile shapes called prototiles; see the box below each tiling result. In particular, our approach is versatile. It can handle domains represented by various forms of grid, e.g., a square grid (left), a hexagon grid (middle), and a square-triangle grid (right).
Abstract
A K-hedral tiling of a 2D finite domain is a covering of the domain with tiles without gaps or overlaps, where each tile is congruent to one of the K distinct shapes called prototiles.
Typically, a forward approach is adopted to produce K-hedral tilings by prescribing a set of prototiles and placing prototile instances (i.e., tiles) to cover the input domain.
However, the prescribed prototile set may not be sufficient to tile the domain (for small K) or may lead to tiling results with excessive prototiles more than needed (for large K).
In this work, we formulate a new tiling problem called inverse tiling for producing K-hedral tilings in 2D finite domains, where the prototile set is inversely modeled to fit the input domain instead of being prescribed.
Since the prototile set is unknown, inverse tiling allows exploring a large search space to discover a minimized number of prototiles for tiling the input domain.
To solve the inverse tiling problem, we propose a computational approach that progressively builds the prototile set while tiling the input domain, starting from a prototile set with a single element.
Once a tiling result is obtained, the approach further reduces the number of prototiles by locally re-tiling the input domain to eliminate prototiles with few instances.
We demonstrate the effectiveness of our inverse tiling approach on a variety of finite domains, evaluate its performance in scalability and K minimization, and compare it quantitatively with forward tiling approaches.
Download
Paper PDF (~21.1M)Supplementary PDF (~3.4M)
Source Code
Video
Results
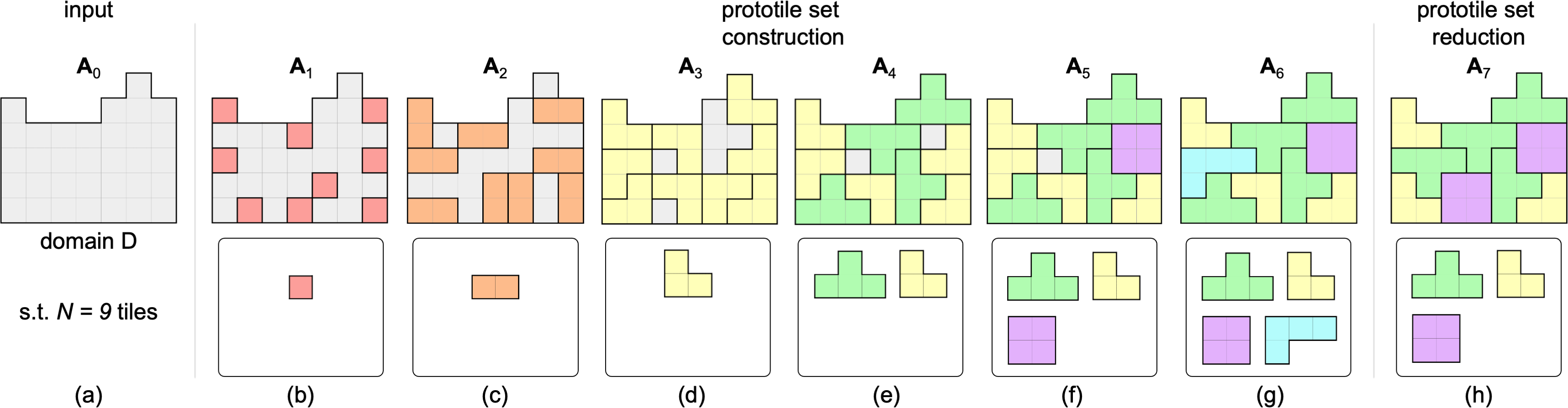
Figure 2:
Overview: our inverse tiling approach consists of two stages: (b-g) prototile set construction and (h) prototile set reduction. Given (a) input domain D, we (b) initialize the prototile set with a single element (i.e., a monomino) and randomly distribute the prototile’s N = 9 instances over the domain. We (c-g) iteratively enlarge the tiles to cover a larger portion of the domain while maintaining congruence of the tile shapes whenever possible to minimize the number of prototiles, until the domain is fully covered by the tiles. (h) We further reduce the number of prototiles by eliminating one prototile (in cyan) with a single instance via locally re-tiling. Note that each prototile and its instances in a tiling state Ai are rendered using the same color to show their correspondence.
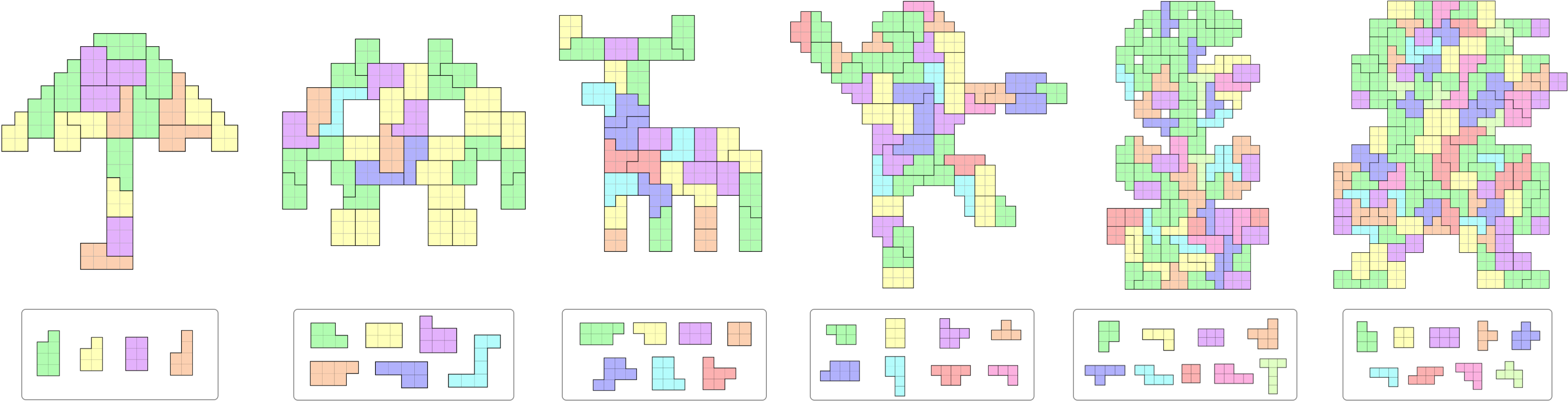
Figure 3:
Tiling results produced by our approach on input square-grid domains of various shapes, from left to right: Umbrella, Robot, Deer, Mega Man, Flower, and Mario.
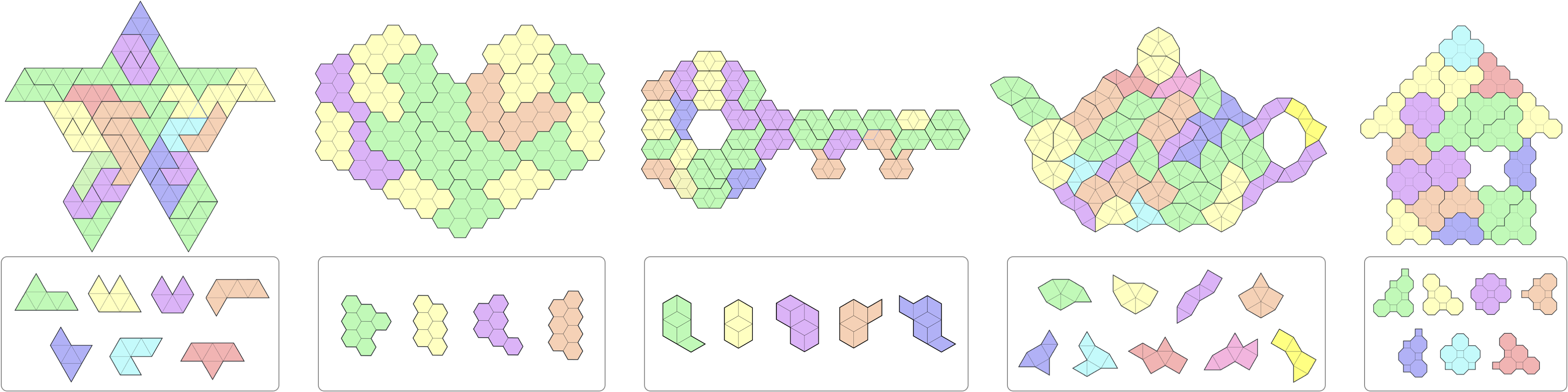
Figure 4:
Tiling results produced by our approach on input domains represented by different kinds of grids, from left to right: a triangle, hexagon, rhombus, square-triangle, and octagon-square grid.
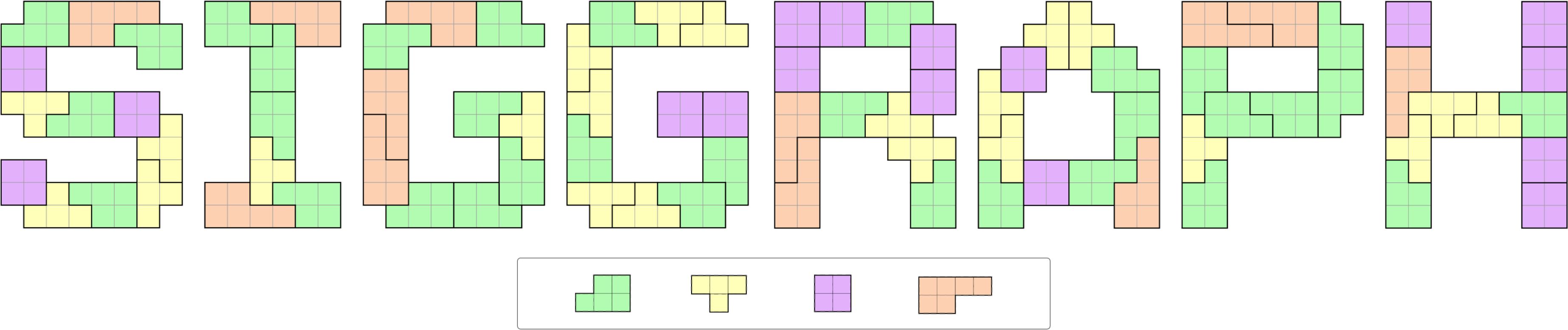
Figure 5:
A tiling result produced by our approach on an input domain SIGGRAPH with 8 disjoint letters.
Figure 6: 2D assembly puzzles designed using our inverse tiling approach. The level of difficulty of the puzzles is related to (a&c) the number (N) of tiles, (a&b) number (K) of prototiles, and (d&e) grid type (square vs hexagon). For each puzzle, we show its component pieces and assembled shape.
Acknowledgments
We thank the reviewers for their valuable comments. This work was supported by the Singapore MOE AcRF Tier 2 Grant (MOE-T2EP20123-0016).
Bibtex
@inproceedings {Chen-2025-InverseTiling,author = {Rulin Chen and Xuyang Ma and Praveer Tewari and Chi-Wing Fu and Peng Song},
title = {Inverse Tiling of 2D Finite Domains},
booktitle = {SIGGRAPH Asia 2025 Conference Papers},
year = {2025}}