Computational Design of High-level Interlocking PuzzlesSIGGRAPH 2022, technical paper |
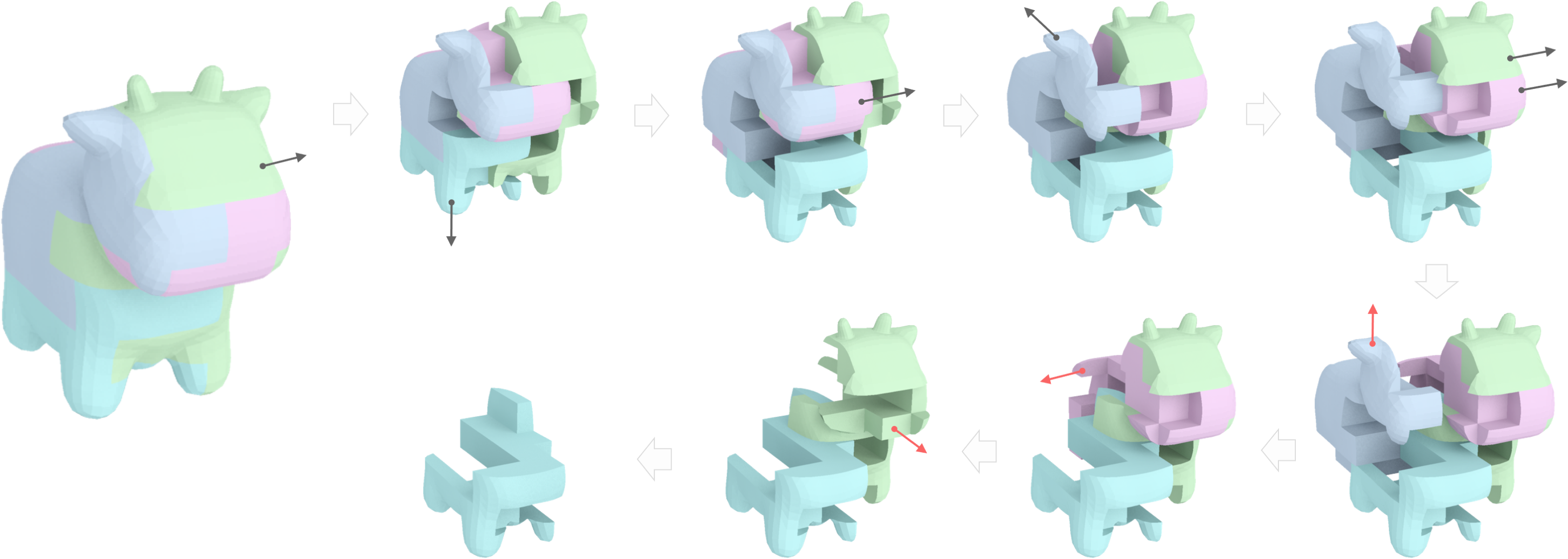
Figure 1: A 4-piece level-6 interlocking puzzle designed by our approach that requires 6 moves to take out the first piece (in blue color). Each sub-figure shows a configuration of the puzzle pieces in the disassembly plan, where arrows indicate the translational direction to move (in black) or remove (in red) a subassembly to reach the next configuration. Note that the two black arrows in the top right subfigure indicate a single move of a subassembly with two parts.
Abstract
Interlocking puzzles are intriguing geometric games where the puzzle pieces are held together based on their geometric arrangement, preventing the puzzle from falling apart. High-level-of-difficulty, or simply high-level, interlocking puzzles are a subclass of interlocking puzzles that require multiple moves to take out the first subassembly from the puzzle. Solving a high-level interlocking puzzle is a challenging task since one has to explore many different configurations of the puzzle pieces until reaching a configuration where the first subassembly can be taken out. Designing a high-level interlocking puzzle with a user-specified level of difficulty is even harder since the puzzle pieces have to be interlocking in all the configurations before the first subassembly is taken out.
In this paper, we present a computational approach to design high-level interlocking puzzles. The core idea is to represent all possible configurations of an interlocking puzzle as well as transitions among these configurations using a rooted, undirected graph called a disassembly graph and leverage this graph to find a disassembly plan that requires a minimal number of moves to take out the first subassembly from the puzzle. At the design stage, our algorithm iteratively constructs the geometry of each puzzle piece to expand the disassembly graph incrementally, aiming to achieve a user-specified level of difficulty. We show that our approach allows efficient generation of high-level interlocking puzzles of various shape complexities, including new solutions not attainable by state-of-the-art approaches.
Download
Paper PDF (~17M)Supplementary PDF (~8M)
Supplementary Results (~35M)
Source Code
Presentation (15-min)
Video
Results
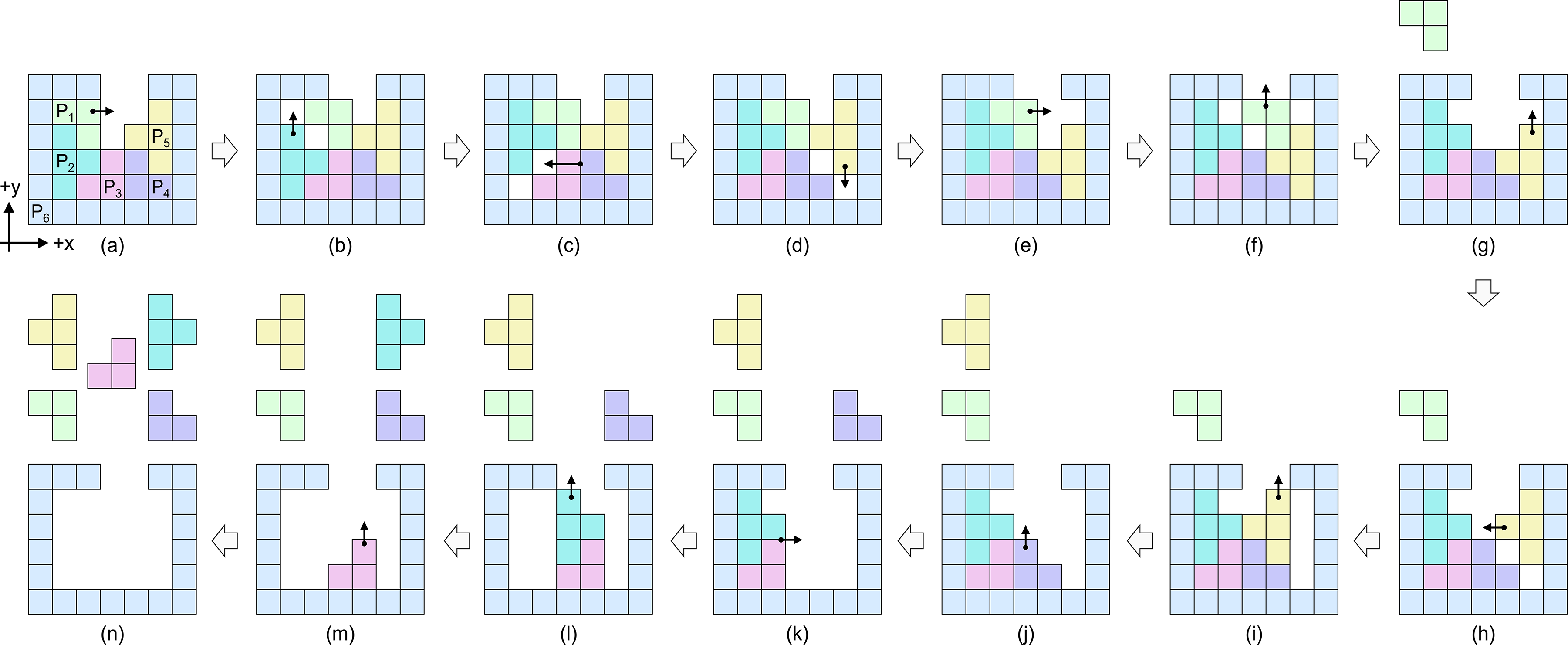
Figure 2: Disassemble a 6-piece level-6 puzzle using a non-monotone and non-linear plan. The kernel disassembly plan is shown in (a-g) while the complete disassembly plan is shown in (a-n). In (g-h), we show disassembled puzzle pieces on top of the puzzle and adjust their positions to avoid overlap.

Figure 3: High-level interlocking puzzles generated by our approach. From left to right and then top to bottom: Cube Frame, Shelf, Spider, Mario, Bunny, Moai, Angry Bird, Owl, Pumpkin, and Squirrel.

Figure 4: Our fabrication results. From top to bottom, Cube, Sofa, Airplane, Cow, and Owl.
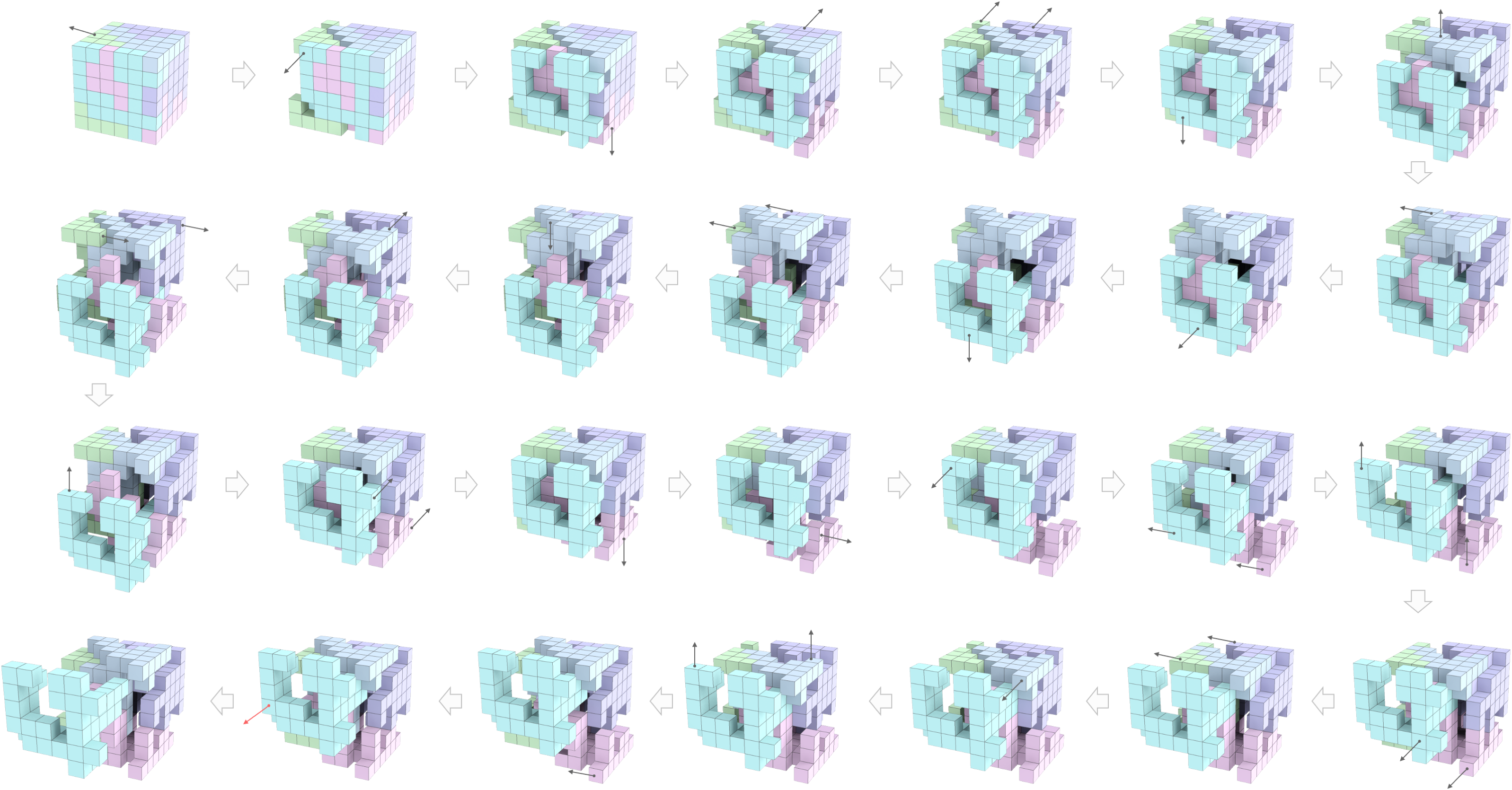
Figure 5: A kernel disassembly plan to take out the first puzzle piece (in cyan) from a 5-piece level-27 6 × 6 × 6 Cube designed by our approach.
Acknowledgments
We thank the reviewers for the valuable comments, David Gontier for sharing the source code of the baseline design approach, Christian Hafner for proofreading the paper, Keenan Crane for the 3D model of Cow, and Thingiverse for the 3D models of Moai and Owl.
This work was supported by the SUTD Start-up Research Grant (Number: SRG ISTD 2019 148), the Swiss National Science Foundation (NCCR Digital Fabrication Agreement #51NF40-141853), and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No 715767 – MATERIALIZABLE).
Bibtex
@article {Chen-2022-HighLevelPuzzle,author = {Rulin Chen and Ziqi Wang and Peng Song and Bernd Bickel},
title = {Computational Design of High-level Interlocking Puzzles},
journal = {ACM Transactions on Graphics (SIGGRAPH)},
volume = {41},
number = {4},
pages = {150:1 -- 150:15},
year = {2022}}